Keywords: tomographic reconstruction, part geometry, shape determination, deformable model, industrial radiography, maximum a posteriori (MAP) reconstruction
It is often desired to accurately verify the geometry and dimensions of a structural component. One way to reach this goal is through tomographic reconstruction of the of part density distribution, which typically requires that the part be radiographed from many different directions. I show that tomographic reconstructions can be obtained from just a few radiographs when the approximate geometry of the part to be examined is known beforehand. The proposed reconstruction algorithm is based on the Bayesian approach to data analysis, which allows one to incorporate prior information in drawing inferences from the data.
The essential feature of the proposed algorithm is a flexible (deformable) geometric model for the part. The model starts from the assumed shape of the part. This geometric shape is then deformed into a final shape whose calculated projections agree with the actual radiographic data. The range of possible deformations is controlled through a prior probability density function of the form exp(-W), where W is the strain energy associated with the deformation. Bayes' law allows one to combine such prior information with the observed radiographic data to obtain the total, or posterior, probability of any given reconstruction. Normally the reconstruction is chosen to maximize the posterior probability, which is designated the MAP solution. The details of the proposed algorithm may be found in Ref. 1.
The deformation process employed in this algorithm is given by a coordinate transformation between the reconstruction coordinates and the coordinates of the prior model. The elastic moduli that determine the deformation strain energy are chosen on the basis of the extent of variability in shape from part to part. Note that the strain energy involved does not correspond to real strain in the part.
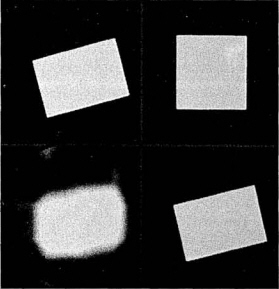
A simple example of reconstruction from four views is shown in Fig. 1. The standard Algebraic Reconstruction Technique (ART) algorithm (lower left) presents a very blurry result that does not lend itself to dimensional measurement. For the present algorithm, the prior model is taken to be a square object (upper right). The MAP reconstruction (lower right) reproduces exactly the original rectangle (upper left) because the square can be transformed into the rectangle through the linear coordinate transformation assumed for this reconstruction. The six transformation parameters are determined as part of the reconstruction process. The relevant dimensions of the rectangle may be calculated from the deformed model.
As a second example, a sausage-shaped object (upper left) reconstructed from five projection using the ART algorithm is presented in Fig. 2 (lower left). With a circular prior model (upper right) the MAP algorithm results in a reasonable reconstruction (lower right). A somewhat different shape is chosen in this example to emphasize the deformation aspect of the algorithm. In actual application, the prior model would presumably be much closer to the actual shape of the part being tested and the final reconstruction would be much better.
In cases in which the projections of the deformed geometric model do not match the actual projections, the reconstruction algorithm can estimate a defect image, which, when added to the deformed model, accurately reproduces the measurements. Both internal and external defects in the part can be seen in this defect image.
| Figure 1. Results for tomographic reconstruction of a tilted rectangle (upper left) based on four parallel projections, equally spaced in angle over 180 deg. The minimum-norm solution is provided by the ART algorithm (lower left); the MAP reconstruction (lower right) is obtained from a square prior model (upper right), rendered flexible by the deformation process described in the text. |
|
| Figure 2. The ART reconstruction (lower left), obtained from five noiseless parallel projections covering 180 deg., poorly reproduces the original sausage-shaped object (upper left). The new algorithm yields the reconstruction (lower right), which more clearly defines the shape of the actual object. It is based on the circular prior model (upper right), which is subjected to a polynomial coordinate transformation of third order, constrained to maintain left-right symmetry. |
|
Go to my publication list
Send e-mail to author at kmh@hansonhub.com